今日推荐开源项目:《幻灯片 fusuma》
今日推荐英文原文:《When to loop? When to recurse?》

今日推荐开源项目:《幻灯片 fusuma》传送门:GitHub链接
推荐理由:简单方便的使用 Markdown 创造幻灯片。你只需要写好想要作为幻灯片展示的 Markdown 并按照顺序整理好目录结构,再写好需要的 CSS 文件之后,这个项目就能够让你简单的使用浏览器展示它们,或者是把它整体导出为一个 pdf 文件。不管怎么说,它都能让你在需要把 Markdown 作为幻灯片展示的时候省下不少功夫。
今日推荐英文原文:《When to loop? When to recurse?》作者:Faith Chikwekwe
原文链接:https://medium.com/@faith.chikwekwe/when-to-loop-when-to-recurse-b786ad8977de
推荐理由:递归可以做循环能做的工作,也能做循环不能做的工作,只有在需要的时候,才应该使用递归——最起码给别人看代码的时候,循环看起来比较好懂。
When to loop? When to recurse?
Well known Google joke featuring recursion
Cracking the Coding Interview states that “All recursive algorithms can [also] be implemented iteratively…” in its section on approaching technical interview problems using recursion.
Solving a Python problem iteratively might include using a for or while loop. These are some of the most common tools used for incremental problem solving in any coding language. Loops are great because a lot of the time, their implementation is intuitive and straightforward.
However, there are times when iterative solutions can turn into barely readable nightmares.

Trying to write highly nested and complicated code on a whiteboard with an interviewer’s inquisitive gaze inspecting your work can be a surefire way to trip yourself up in a technical interview.
While switching from looping to recursion will not always make your code better, it is a great tool to have in your toolbox.
For a while, I was afraid of learning recursion. Upon learning that problems with a recursive solution inevitably have an iterative one as well, I was fixated on trying to solve every technical problem with loops.
However, as my technical interview skills grew, I encountered many LeetCode and HackerRank problems that cried out for recursion with their complexity. It was time to broaden the tools at my disposal.
What are Loops?
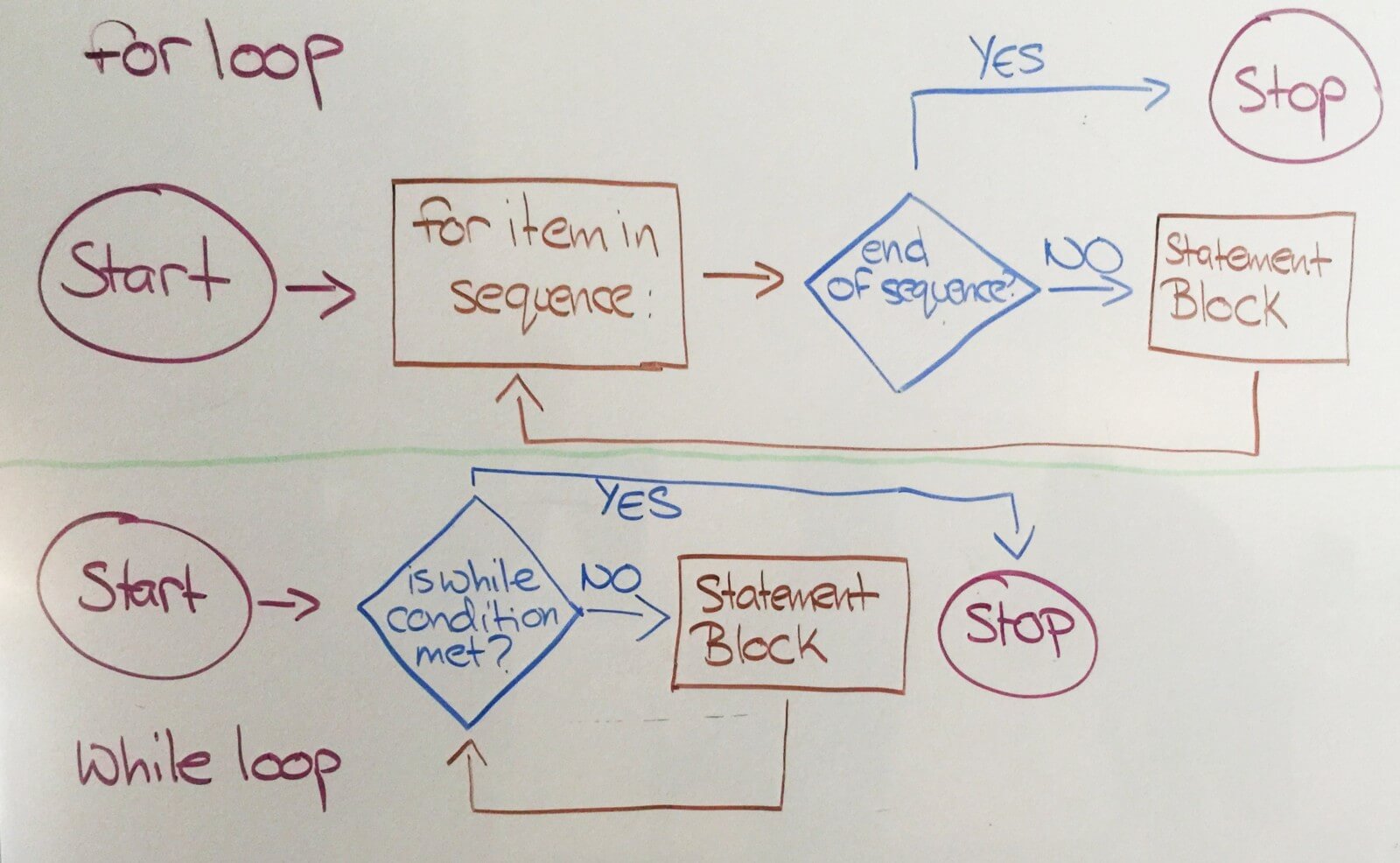
Diagram of a for loop and a while loop.
A loop is used to perform a repetitive block of code as many times as necessary for the program.
for name in name_list: # we go over every name in the list
name = name.title() # we change every name
counter += 1 # each time, we add 1 more to the counter
We might also need to loop for an undetermined number of times or until a certain condition is met. This might be a good time to use a while loop.
def length(self):
"""Return the length of this linked list by traversing its nodes."""
node_count = 0 # initial count is zero
current = self.head # start at the head
# Loop through all nodes
while current is not None:
current = current.next
# add one to the counter each time
node_count += 1
# return the total length
return node_count
Okay, so what is Recursion?

Image from https://medium.com/@williambdale/recursion-the-pros-and-cons-76d32d75973a
A big difference between recursion and iteration is the way that they end. While a loop executes the block of code, checking each time to see if it is at the end of the sequence, there is no such sequential end for recursive code.
Like the horrifying Winnie the Pooh comic above, a recursive function could go on forever without a condition to put it out of its misery.

Showing the base case and the recursive call in a recursive function on the factorial example. Image from https://www.slideshare.net/alhazmy13/data-structures-part5-recursion
A recursive function like the one above consists of two parts: the recursive call and the base case.
The base case (or bases cases sometimes) is the condition that checks to see if we have gotten the information that we need out of our function. Every recursive function should have at least one base case, though there may be multiple.
In the factorial example above, we have reached the end of our necessary recursive calls when we get to the number 0.
The recursive call as you may have suspected is when the function calls itself adding to the recursive call stack.
Stacks are LIFO (Last In First Out) objects meaning that the last item that was added to the top of the stack is the first one to be removed from the stack later on.

Diagram from https://medium.com/@charlie.b.ohara/recursion-revealed-f8543e4dad1c
When Should I Use Recursion?
Recursion is made for solving problems that can be broken down into smaller, repetitive problems. It is especially good for working on things that have many possible branches, and are too complex for an iterative approach.One good example of this would be searching through a file system. When you start at the root folder, and then you could search through all the files and folders within that one. After that you would enter each folder and search through each folder inside of that.
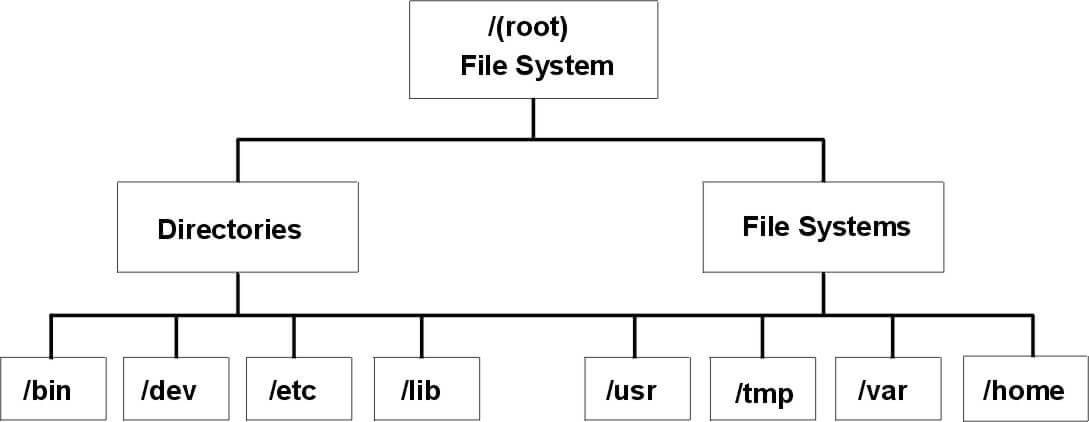
Recursion works well for this type of structure, because you can search multiple branching paths without having to include many different checks and conditions for every possibility.
For those of your who are familiar with data structures, you might notice that the image above of the file system looks a lot like a tree structure.
Trees and graphs are another time when recursion is the best and easiest way to do traversal.
Should I Always Use Recursion?
Recursion seems really useful! Maybe I should use it all the time?Well, like anything recursion is best in doses. Recursion is a useful tool, but it can increase memory usage.
So let’s go back to the factorial call stack image from above. Every time we add a new call to the stack, we are increasing the amount of memory that we are using. If we are analyzing the algorithm using Big O notation, then we might note that this increases our space complexity.
There are times when we might want to pay this cost in order to get a short, useful algorithm, like when we are traversing a tree. But there are other times, when there may be better, more efficient ways of solving this problem.
For many small projects, the call stack won’t hamper you program very much. However, once your program starts making many recursive calls, then you might want to consider the potential impact of your large call stack.

Stack of Books. Photo by John-Mark Smith on Unsplash
Another thing to consider is that understanding and reading your code might sometimes be easier to do in an iterative solution.
Using recursion is great because it takes many of the incremental sub problems out of your hands.
But when you are try to fully understand the sub problems that you are solving and how they are being solved, it might be worth implementing an iterative solution. If this is not a feasible route, then at the very least diagram the recursive process undertaken by your code to deepen your knowledge.
下载开源日报APP:https://openingsource.org/2579/
加入我们:https://openingsource.org/about/join/
关注我们:https://openingsource.org/about/love/
