今日推薦開源項目:《代碼貪吃蛇 quinesnake》
今日推薦英文原文:《An intro to Algorithms (Part II): Dynamic Programming》

今日推薦開源項目:《代碼貪吃蛇 quinesnake》傳送門:GitHub鏈接
推薦理由:在假期里打發時間的不錯項目——讓你一邊娛樂一邊在代碼中遨遊。這可一點都沒說錯,你能在代碼里玩貪吃蛇,如果你把那些代碼都無視掉的話,這就是個普通的貪吃蛇遊戲。當然了,好玩歸好玩,如果你想要讀懂源代碼的話,還是去看那個有注釋的版本比較好,你不會想在那團不明所以的東西里尋找邏輯的。
今日推薦英文原文:《An intro to Algorithms (Part II): Dynamic Programming》作者:Meet Zaveri
原文鏈接:https://medium.freecodecamp.org/an-intro-to-algorithms-dynamic-programming-dd00873362bb
推薦理由:介紹動態規劃演算法。有的時候演算法會解決一些完全重複的問題——它得到相同的輸入,然後拿出相同的輸出。而這個演算法能幫你節省下一些花在這上面的時間
An intro to Algorithms (Part II): Dynamic Programming
Suppose you are doing some calculation using an appropriate series of input. There is some computation done at every instance to derive some result. You don』t know that you had encountered the same output when you had supplied the same input. So it』s like you are doing re-computation of a result that was previously achieved by specific input for its respective output.But what』s the problem here? Thing is that your precious time is wasted. You can easily solve the problem here by keeping records that map previously computed results. Such as using the appropriate data structure. For example, you could store input as key and output as a value (part of mapping).
Those who cannot remember the past are condemned to repeat it. ~Dynamic ProgrammingNow by analyzing the problem, store its input if it』s new (or not in the data structure) with its respective output. Else check that input key and get the resultant output from its value. That way when you do some computation and check if that input existed in that data structure, you can directly get the result. Thus we can relate this approach to dynamic programming techniques.
Diving into dynamic programming
In a nutshell, we can say that dynamic programming is used primarily for optimizing problems, where we wish to find the 「best」 way of doing something.A certain scenario is like there are re-occurring subproblems which in turn have their own smaller subproblems. Instead of trying to solve those re-appearing subproblems, again and again, dynamic programming suggests solving each of the smaller subproblems only once. Then you record the results in a table from which a solution to the original problem can be obtained.
For instance, the Fibonacci numbers 0,1,1,2,3,5,8,13,… have a simple description where each term is related to the two terms before it. If F(n) is the nth term of this series then we have F(n) = F(n-1) + F(n-2). This is called a recursive formula or a recurrence relation. It needs earlier terms to have been computed in order to compute a later term.
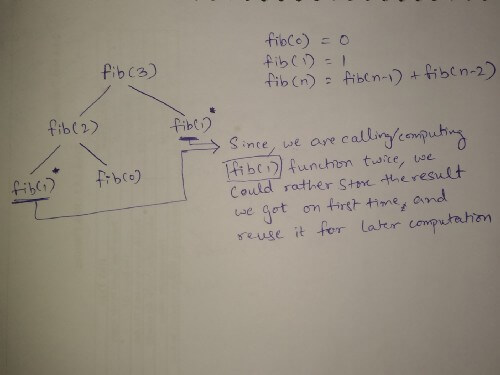
The majority of Dynamic Programming problems can be categorized into two types:
- Optimization problems.
- Combinatorial problems.
An approach to solve: top-down vs bottom-up
There are the following two main different ways to solve the problem:Top-down: You start from the top, solving the problem by breaking it down. If you see that the problem has been solved already, then just return the saved answer. This is referred to as Memoization.
Bottom-up: You directly start solving the smaller subproblems making your way to the top to derive the final solution of that one big problem. In this process, it is guaranteed that the subproblems are solved before solving the problem. This can be called Tabulation (table-filling algorithm).
In reference to iteration vs recursion, bottom-up uses iteration and the top-down uses recursion.

The visualization displayed in the image is not correct acc. to theoretical knowledge, but I have displayed in an understandable manner
Here there is a comparison between a naive approach vs a DP approach. You can see the difference by the time complexity of both.
Memoization: Don』t forget
Jeff Erickson describes in his notes, for Fibonacci numbers:The obvious reason for the recursive algorithm』s lack of speed is that it computes the same Fibonacci numbers over and over and over.

From Jeff Erickson』s notes CC: http://jeffe.cs.illinois.edu/
We can speed up our recursive algorithm considerably just by writing down the results of our recursive calls. Then we can look them up again if we need them later.
Memoization refers to the technique of caching and reusing previously computed results.
If you use memoization to solve the problem, you do it by maintaining a map of already solved subproblems (as we earlier talked about the mapping of key and value). You do it 「top-down」 in the sense that you solve the 「top」 problem first (which typically recurses down to solve the sub-problems).
Pseudocode for memoization:

So using recursion, we perform this with extra overhead memory (i.e. here lookup) to store results. If there is a value stored in the lookup, we return it directly or we add it to lookup for that specific index.
Remember that there is a tradeoff of extra overhead with respect to the tabulation method.
However, if you want more visualizations for memoization, then I suggest looking into this video(https://www.youtube.com/watch?v=Taa9JDeakyU).

In a top-down manner.
Tabulation: Filling up in tabular form
But once we see how the array (memoized solution) is filled, we can replace the recursion with a simple loop that intentionally fills the array in order, instead of relying on the complicated recursion to do it for us 『accidentally』.
From Jeff Erickson』s notes CC: http://jeffe.cs.illinois.edu/
Tabulation does it in 「bottom-up」 fashion. It』s more straight forward, it does compute all values. It requires less overhead as it does not have to maintain mapping and stores data in tabular form for each value. It may also compute unnecessary values. This can be used if all you want is to compute all values for your problem.
Pseudocode for tabulation:

Pseudocode with Fibonacci tree
As you can see pseudocode (right side) in an image, it does iteration (i.e. loops over till the end of an array). It simply starts with fib(0),fib(1),fib(2),… So with the tabulation approach, we can eliminate the need for recursion and simply return the result with looping over elements.
Looking back in history
Richard bellman was the man behind this concept. He came up with this when he was working for RAND Corporation in the mid-1950s. The reason he chose this name 「dynamic programming」 was to hide the mathematics work he did for this research. He was afraid his bosses would oppose or dislike any kind of mathematical research.Okay, so the word 『programming』 is just a reference to clarify that this was an old-fashioned way of planning or scheduling, typically by filling in a table (in a dynamic manner rather than in a linear way) over the time rather than all at once.
下載開源日報APP:https://openingsource.org/2579/
加入我們:https://openingsource.org/about/join/
關注我們:https://openingsource.org/about/love/
