每天推薦一個 GitHub 優質開源項目和一篇精選英文科技或編程文章原文,歡迎關注開源日報。交流QQ群:202790710;微博:https://weibo.com/openingsource;電報群 https://t.me/OpeningSourceOrg

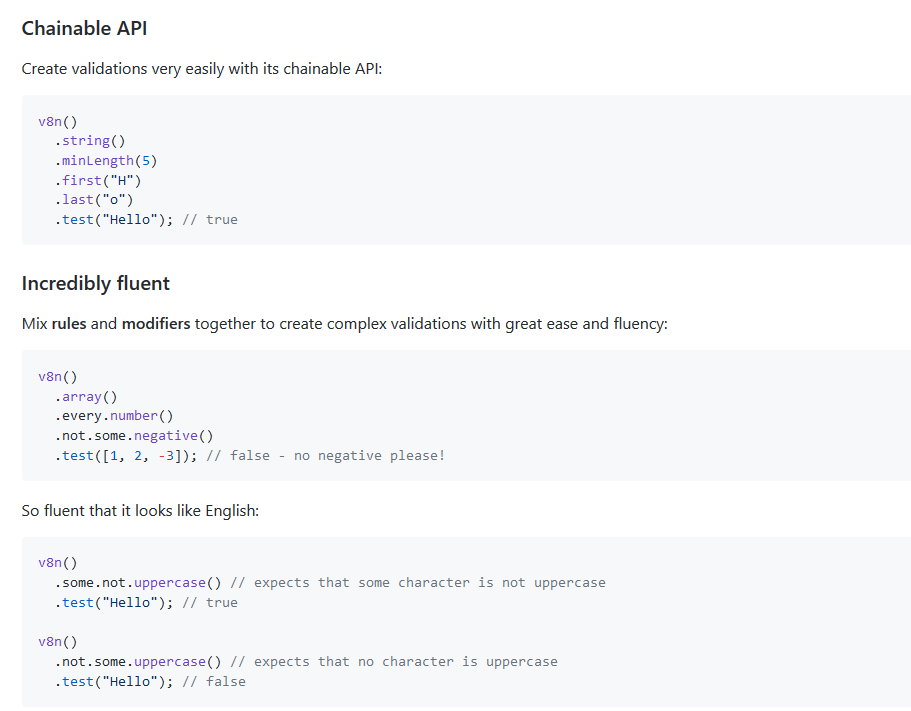
今日推薦開源項目:《JS 驗證庫 v8n》傳送門:GitHub鏈接
推薦理由:這是一個可以用來做各種各樣細的驗證的庫,它裡面的語法看起來和普通的語法很像所以很容易就能理解,而且它的確提供了各種各樣方面的驗證方式,從檢查所有的字母是不是都是小寫到字元串的開頭結尾,有興趣的朋友可以嘗試一下。
今日推薦英文原文:《Algorithms: Common edge cases in JS》作者:Jeremy Gottfried
原文鏈接:https://medium.com/jeremy-gottfrieds-tech-blog/algorithms-common-edge-cases-in-js-ce35a2d47674
推薦理由:極端情況,有的情況興許你的程序一百年也見不到一次,但是為了預防可能出現的各種情況,我們還是應當改進程序以應對極端情況
Algorithms: Common edge cases in JS
Algorithms are the bedrock of computer programming. Algorithms are built to handle specific data structures with a range of accepted parameters. An edge case is a problem or situation that occurs only at an extreme (maximum or minimum) operating parameter. As programmers, how can we predict these cases in order to protect our app from breaking?
I will demonstrate some common edge cases in a basic bubble sort algorithm:
// bubbleSort.js
function bubbleSort(array) {
var swapped;
do {
swapped = false;
for(var i = 0; i < array.length; i++) {
if(array[i] > array[i + 1]) {
swap(array, i, i + 1);
swapped = true;
}
}
} while(swapped);
return array;
}function swap(array, i, j) {
var temp = array[i];
array[i] = array[j];
array[j] = temp;
}1. Accepted data structure
The first major edge case is the unaccepted data structure. My bubble sort algorithm only works predictably for arrays. Javascript will not prevent you from inputting other data structures in the function, such as normal objects. For example, what happens if I input this object:
var obj = {0: 0,
1: 1,
2: 2,
3: 3}
This will do some very strange things inside the for loop, but ultimately, our algorithm will return the original object.
--> obj
That may not be what we want! If the algorithm is going to be truly fool proof, we should test that our data structure is an array, and handle it somehow. Here I will return false so that we can handle unwanted data structures as an error in our program:
if (!Array.isArray(arr)) {
return false
}
This will also return false for falsey values like null or undefined.
2. Emptiness
An empty array would not break this specific sorting algorithm, but empty values are something important to look out for:
bubbleSort([]) --> []
In the context of many programs, we want to handle an empty array differently so that it doesn』t break something in our program further down the line:
if (!arr[0]) {
return false
}
or
if (arr.length === 0) {
return false
}
For algorithms that accept different data structures and types, we should also look out for emptiness. Here are some common ones:
var str = ''
var obj = {}
var arr = []
var num = 0
If our algorithm iterates through nested data structures, we may also want to check for nested emptiness like this:
[[],[],[],[[]],[[[]]]]
3. Accepted types
The next big case to test for is accepted types inside our array. Our bubbleSort algorithm sorts strings based on their Unicode values. That means that capital letters will go before lowercase:
bubbleSort([a,A,b,B]) ---> [A,B,a,b]
If we want the algorithm to sort strings independent of capitalization, we may want to handle that:
if (arr[j-1].toLowerCase > arr[j].toLowerCase) {
var temp = arr[j-1];
arr[j-1] = arr[j];
arr[j] = temp;
}
Another case you may want to handle are string numbers vs normal numerical values. Here is one strange example of this:
2 > '2' ---> false 2 < '2' ---> false 2 === '2' ---> false 2 == '2' ---> true
In the case of two equal numbers, where one is a string, the only operator that evaluates to true is == . It gets even more tricky if there is a letter in the numerical string.
1 > '1a' ---> false 1 < '1a' ---> false 1 === '1a' ---> false 1 == '1a' ---> false 2 > '1a' ---> false 2 < '1a' ---> false
This could lead to some strange results in our sorting algorithm. Therefore, we may want to only accept numbers and not strings, or handle the different types separately.
Another type to be aware of is the boolean value. true is loosely equal to 1 while false is loosely equal to 0 .
true == 1 ---> true false == 0 ---> true true > false ---> true true < 2 ---> true true < 'a' ---> false false < 'a' ---> false
We may not want to allow boolean values in our algorithm, especially if we are sorting an array of strings. This includes falsey values like null, undefined and NaN , which will all act strange when passed into a comparison operator.
The falsey data types all act differently in the comparison operators:
null < 2 ---> true null == 1 ---> false null > 0 ---> false null === null ---> true undefined < 2 ---> false undefined > 0 ---> false undefined == 1 --> false undefined === undefined ---> true NaN === NaN ---> false NaN > 0 ---> false NaN < 2 ---> false NaN == 1 ---> false
You may want to exclude these from your sorting algorithm.
4. Large Values
In our case, we should be looking out for extremely large arrays. What happens if our function is given an array with length greater than 1 x 10¹⁰⁰?
Here is where Big O notation comes in.
Big O complexity
Big O complexity is a measure of algorithm efficiency. It makes a big difference when we are dealing with large data sets. Big O has two variables — time and memory space. Memory is important because it can be break our algorithm if large amounts of data are passed as parameters. Every computer program stores data in stack and heap memory. Stack memory is much faster to access but there』s less of it. How does this relate to algorithms?
Let』s answer this with two versions of bubble sort, recursive and iterative —
// bubbleSort.js
function swap(array, i, j) {
var temp = array[i];
array[i] = array[j];
array[j] = temp;
}/// Bubble Sort using for loops
function bubbleSort(array) {
var swapped;
do {
swapped = false;
for(var i = 0; i < array.length; i++) {
if(array[i] > array[i + 1]) {
swap(array, i, i + 1);
swapped = true;
}
}
} while(swapped);
return array;
}// Bubble sort using recursion
var swapped = true
function recursiveSwapping(arr, i = 0) {
var len = arr.length;
if (i >= len) {
return arr
}
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);
swapped = true
}
return recursiveSwapping(arr, i + 1)
}
function recursiveBubbleSort(arr) {
if (!swapped) {
return arr
}
swapped = false
recursiveSwapping(arr, i = 0)
return recursiveBubbleSort(arr)
}
These two examples use the same exact algorithm, but the memory is handled differently. The recursive version of the algorithm uses stack memory, and will therefore break with a stack overflow error if the length of the array is very large. This is because the stack keeps track of every call of recursiveSwappinguntil the original call resolves. The iterative version of the function doesn』t face stack overflow issues.
In theory, the recursive version shouldn』t face memory issues either. Many lower level languages allow something called tail-call optimization, which makes it possible to to write recursive functions with 0(1) memory complexity. Until recently, JS did not allow tail call optimization, but in ECMAScript 6 you can enable it in strict mode. Simply type 'use strict』 at the top of the file, and you will be able to write recursively without running into stack overflow errors.
'use strict'
Just make sure that your recursive function calls are written in the last line, or tail, of your function like in the function below.
function recursiveSwapping(arr, i = 0) {
var len = arr.length;
if (i >= len) {
return arr
}
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);
swapped = true
}
// tail call below
return recursiveSwapping(arr, i + 1)
}
5. Some other edge cases to keep in mind
- Odd/even — numbers and string length
- Negative numbers
- Special characters
- Duplicate elements
- Length of 1
- Long string or large number
- Null or Falsey values
每天推薦一個 GitHub 優質開源項目和一篇精選英文科技或編程文章原文,歡迎關注開源日報。交流QQ群:202790710;微博:https://weibo.com/openingsource;電報群 https://t.me/OpeningSourceOrg
